∫ − ∞ ∞ e − x 2 d x \displaystyle\int_{-\infin}^{\infin}e^{-x^2}dx ∫−∞∞​e−x2dx 是一个比较常见的无穷积分，在许多领域有着重要应用。

  在此介绍几种巧妙的解法，供读者欣赏。 为了您更好的阅读体验，请使用电脑浏览。

   ( ∫ − ∞ ∞ e − x 2 d x ) 2 = ∫ − ∞ ∞ e − x 2 d x ∫ − ∞ ∞ e − y 2 d y = ∫ − ∞ ∞ ∫ − ∞ ∞ e − ( x 2 + y 2 ) d x d y ( 极坐标变换 ) = ∫ 0 2 π ∫ 0 ∞ e − r 2 r d r d θ = ( ∫ 0 2 π d θ ) ( 1 2 ∫ 0 ∞ e − r 2 d r 2 ) = 2 π 1 2 = π ∴    ∫ − ∞ ∞ e − x 2 d x = π   . \begin{aligned}\big(\int_{-\infin}^{\infin}e^{-x^2}dx\big)^2&=\int_{-\infin}^{\infin}e^{-x^2}dx\int_{-\infin}^{\infin}e^{-y^2}dy\\&=\int_{-\infin}^{\infin}\int_{-\infin}^{\infin}e^{-(x^2+y^2)}dxdy \quad(\text{极坐标变换})\\&=\int_{0}^{2\pi}\int_{0}^{\infin}e^{-r^2}rdrd\theta\\&=\big(\int_{0}^{2\pi}d\theta\big)\big(\frac{1}{2}\int_{0}^{\infin}e^{-r^2}dr^2\big)\\&=2\pi\frac{1}{2}=\pi\\ \therefore \,\,\int_{-\infin}^{\infin}e^{-x^2}dx&=\sqrt{\pi}\,.\end{aligned} (∫−∞∞​e−x2dx)2∴∫−∞∞​e−x2dx​=∫−∞∞​e−x2dx∫−∞∞​e−y2dy=∫−∞∞​∫−∞∞​e−(x2+y2)dxdy(极坐标变换)=∫02π​∫0∞​e−r2rdrdθ=(∫02π​dθ)(21​∫0∞​e−r2dr2)=2π21​=π=π ​.​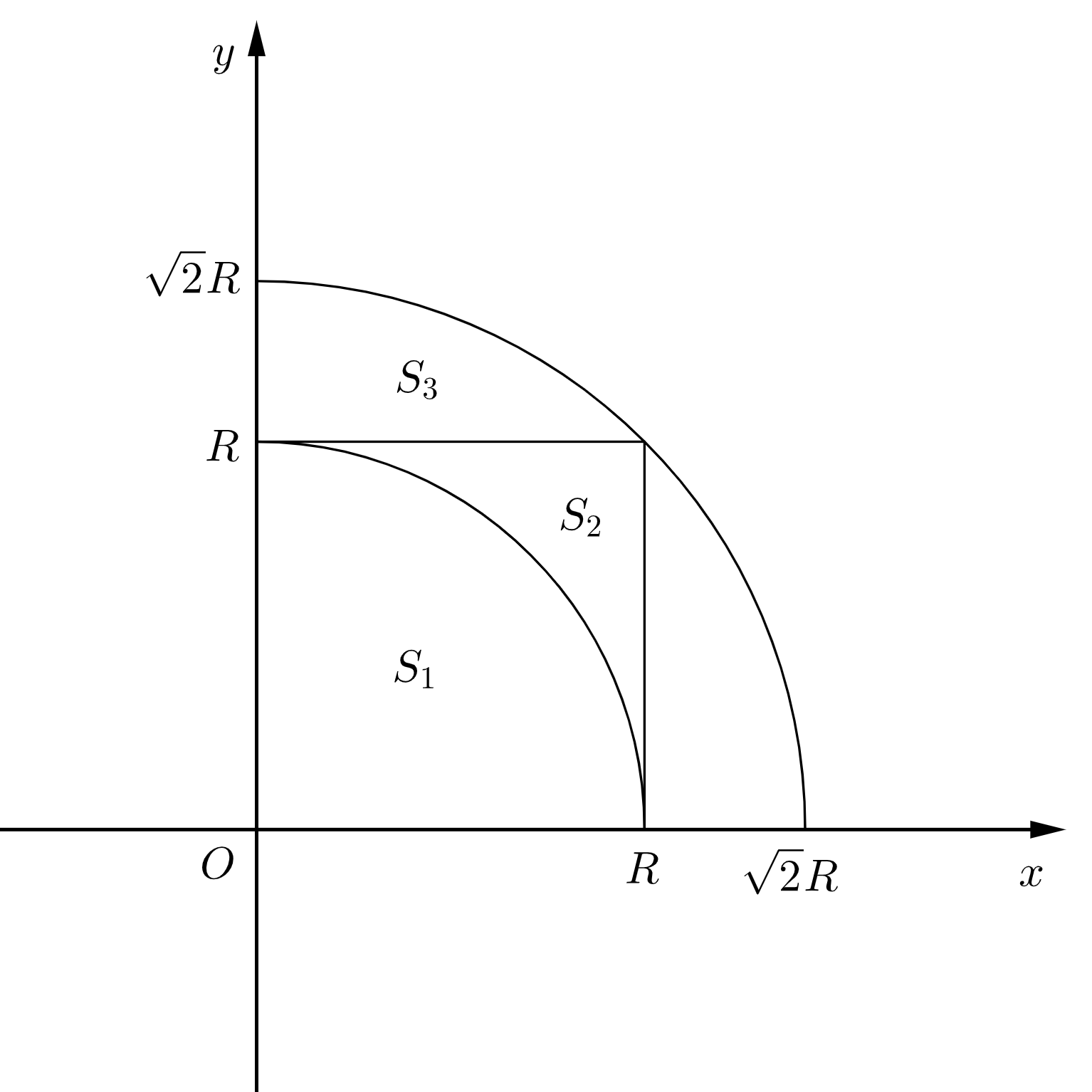

S 1 = { ( x , y )   ∣   x 2 + y 2 ≤ R 2 } S 2 = { ( x , y )   ∣   0 ≤ x ≤ R ,   0 ≤ y ≤ R } S 3 = { ( x , y )   ∣   x 2 + y 2 ≤ 2 R 2 }   \begin{aligned}S_1&=\{(x,y)\,|\,x^2+y^2\leq R^2\}\\S_2&=\{(x,y)\,|\,0\leq x \leq R,\,0\leq y \leq R\}\\S_3&=\{(x,y)\,|\,x^2+y^2\leq 2R^2\}\\\,\end{aligned} S1​S2​S3​​={(x,y)∣x2+y2≤R2}={(x,y)∣0≤x≤R,0≤y≤R}={(x,y)∣x2+y2≤2R2}​     ( ∫ 0 R e − x 2 d x ) 2 = ∫ 0 R e − x 2 d x ∫ 0 R e − y 2 d y = ∫ 0 R ∫ 0 R e − ( x 2 + y 2 ) d x d y = ∬ S 2 e − ( x 2 + y 2 ) d x d y \begin{aligned}\big(\int_{0}^{R}e^{-x^2}dx\big)^2&=\int_{0}^{R}e^{-x^2}dx\int_{0}^{R}e^{-y^2}dy\\&=\int_{0}^{R}\int_{0}^{R}e^{-(x^2+y^2)}dxdy\\&=\iint_{S_2}e^{-(x^2+y^2)}dxdy\end{aligned} (∫0R​e−x2dx)2​=∫0R​e−x2dx∫0R​e−y2dy=∫0R​∫0R​e−(x2+y2)dxdy=∬S2​​e−(x2+y2)dxdy​

   ∵ e − ( x 2 + y 2 ) ≥ 0 ∴ ∬ S 1 e − ( x 2 + y 2 ) d x d y ≤ ∬ S 2 e − ( x 2 + y 2 ) d x d y ≤ ∬ S 3 e − ( x 2 + y 2 ) d x d y \begin{aligned}&\because e^{-(x^2+y^2)}\geq 0 \\ &\therefore \iint_{S_1}e^{-(x^2+y^2)}dxdy\leq\iint_{S_2}e^{-(x^2+y^2)}dxdy\leq\iint_{S_3}e^{-(x^2+y^2)}dxdy\end{aligned} ​∵e−(x2+y2)≥0∴∬S1​​e−(x2+y2)dxdy≤∬S2​​e−(x2+y2)dxdy≤∬S3​​e−(x2+y2)dxdy​

    ∬ S 1 e − ( x 2 + y 2 ) d x d y = ∫ 0 π / 2 ∫ 0 R e − r 2 r d r d θ = ( ∫ 0 π / 2 d θ ) ( 1 2 ∫ 0 R e − r 2 d r 2 ) = π 4 ( 1 − e − R 2 ) \begin{aligned}\iint_{S_1}e^{-(x^2+y^2)}dxdy&=\int_{0}^{\pi/2}\int_{0}^{R}e^{-r^2}rdrd\theta\\&=\big(\int_{0}^{\pi/2}d\theta\big)\big(\frac{1}{2}\int_{0}^{R}e^{-r^2}dr^2\big)\\&=\frac{\pi}{4}(1-e^{-R^2})\end{aligned} ∬S1​​e−(x2+y2)dxdy​=∫0π/2​∫0R​e−r2rdrdθ=(∫0π/2​dθ)(21​∫0R​e−r2dr2)=4π​(1−e−R2)​

同理   ∬ S 3 e − ( x 2 + y 2 ) d x d y = π 4 ( 1 − e − 2 R 2 )   . 则    π 4 ( 1 − e − R 2 ) ≤ ∬ S 2 e − ( x 2 + y 2 ) d x d y ≤ π 4 ( 1 − e − 2 R 2 )   . 两边取极限   R → ∞ ，则   ( ∫ 0 ∞ e − x 2 d x ) 2 = ∬ R 2 e − ( x 2 + y 2 ) d x d y = π 4 . 所以   ∫ 0 ∞ e − x 2 d x = π 2   . \begin{aligned}\\&\text{同理}\,\iint_{S_3}e^{-(x^2+y^2)}dxdy=\frac{\pi}{4}(1-e^{-2R^2})\,.\\&\text{则}\,\, \frac{\pi}{4}(1-e^{-R^2})\leq\iint_{S_2}e^{-(x^2+y^2)}dxdy\leq\frac{\pi}{4}(1-e^{-2R^2})\,.\\&\text{两边取极限}\,R\to\infin\text{，则}\,\Big(\int_{0}^{\infin}e^{-x^2}dx\Big)^2=\iint_{R^2}e^{-(x^2+y^2)}dxdy=\frac{\pi}{4}.\\&\text{所以}\,\int_{0}^{\infin}e^{-x^2}dx=\frac{\sqrt{\pi}}{2} \,.\end{aligned} ​同理∬S3​​e−(x2+y2)dxdy=4π​(1−e−2R2).则4π​(1−e−R2)≤∬S2​​e−(x2+y2)dxdy≤4π​(1−e−2R2).两边取极限R→∞，则(∫0∞​e−x2dx)2=∬R2​e−(x2+y2)dxdy=4π​.所以∫0∞​e−x2dx=2π ​​.​

考虑曲线   z = e − x 2   绕   z   轴旋转一周生成的旋转体的体积，由高数知识 \begin{aligned}\text{考虑曲线}\, z=e^{-x^2}\, \text{绕}\, z\, \text{轴旋转一周生成的旋转体的体积，由高数知识}\end{aligned} 考虑曲线z=e−x2绕z轴旋转一周生成的旋转体的体积，由高数知识​ V = ∫ 0 1 π x 2 d z = π ∫ 0 1 ( − ln ⁡ z ) d z = π ( z − z ln ⁡ z )   ∣ 0 1 = π ( 1 − lim ⁡ z → 0 + ( z − z ln ⁡ z ) ) = π \begin{aligned}V&= \int_0^{1}\pi x^2dz\\&=\pi \int_0^{1}(-\ln z)dz\\&=\pi (z-z\ln z)\,\Big|_0^1\\&=\pi (1-\lim_{z\to 0^{+}}(z-z\ln z))\\&=\pi\end{aligned} V​=∫01​πx2dz=π∫01​(−lnz)dz=π(z−zlnz)∣∣∣​01​=π(1−z→0+lim​(z−zlnz))=π​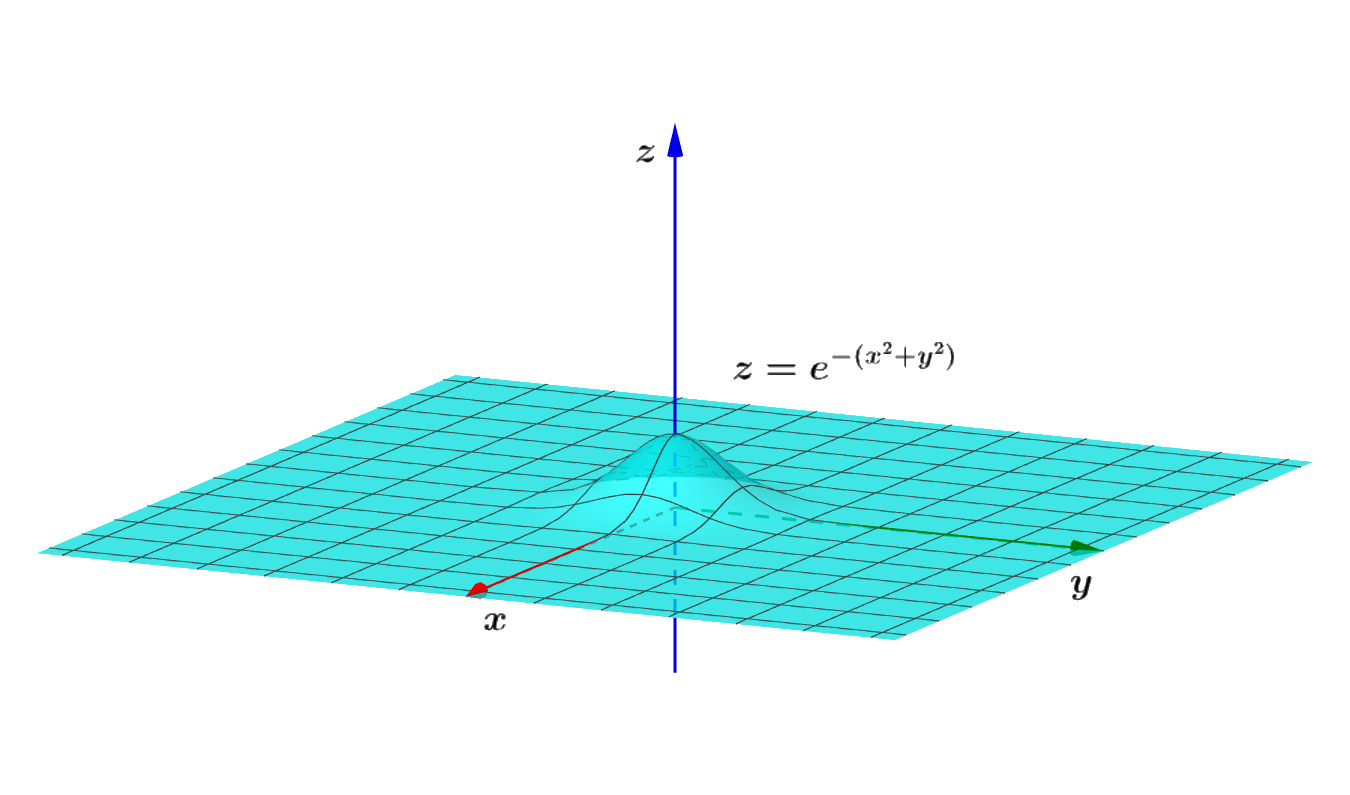

旋转体在几何上的表示如图所示，旋转生成的曲面方程为   z = e − ( x 2 + y 2 ) . 旋转体的体积也可以理解为曲面   z = e − ( x 2 + y 2 ) 与   x O y   之间部分的体积，即 \begin{aligned}&\text{旋转体在几何上的表示如图所示，旋转生成的曲面方程为} \,z=e^{-(x^2+y^2)}. \\ &\text{旋转体的体积也可以理解为曲面} \,z=e^{-(x^2+y^2)} \text{与}\,xOy\,\text{之间部分的体积，即}\end{aligned} ​旋转体在几何上的表示如图所示，旋转生成的曲面方程为z=e−(x2+y2).旋转体的体积也可以理解为曲面z=e−(x2+y2)与xOy之间部分的体积，即​ π = V = ∬ R 2 e − ( x 2 + y 2 ) d x d y = ∫ − ∞ ∞ e − x 2 d x ∫ − ∞ ∞ e − y 2 d y = ( ∫ − ∞ ∞ e − x 2 d x ) 2 \pi=V=\iint_{R^2}e^{-(x^2+y^2)}dxdy=\int_{-\infin}^{\infin}e^{-x^2}dx\int_{-\infin}^{\infin}e^{-y^2}dy=\big(\int_{-\infin}^{\infin}e^{-x^2}dx\big)^2 π=V=∬R2​e−(x2+y2)dxdy=∫−∞∞​e−x2dx∫−∞∞​e−y2dy=(∫−∞∞​e−x2dx)2 则 ∫ − ∞ ∞ e − x 2 d x = π . \begin{aligned} \text{则} \int_{-\infin}^{\infin}e^{-x^2}dx=\sqrt{\pi}.\end{aligned} 则∫−∞∞​e−x2dx=π ​.​

令   f ( t ) = ∫ 0 ∞ e − x 2 t d x ，对   f ( t )   作拉普拉斯变换，令 \begin{aligned}&\text{令}\,f(t)=\int_0^{\infin}e^{-x^2t}dx\text{，对}\,f(t)\,\text{作拉普拉斯变换，令}\end{aligned} ​令f(t)=∫0∞​e−x2tdx，对f(t)作拉普拉斯变换，令​    F ( s ) = L [ f ( t ) ] = ∫ 0 ∞ L [ e − x 2 t ] t   d x = ∫ 0 ∞ 1 s + x 2 d x = 1 s ∫ 0 ∞ 1 1 + ( x s ) 2 d ( x s ) ( let    u = x s ) = 1 s arctan ⁡ u   ∣ 0 ∞ = π 2 s − 1 2 \begin{aligned}F(s)=\mathscr{L}[f(t)]&=\int_0^{\infin}\mathscr{L}[e^{-x^2t}]_t\,dx\\&=\int_0^{\infin}\frac{1}{s+x^2}dx\\&=\frac{1}{\sqrt{s}}\int_{0}^{\infin}\frac{1}{1+(\displaystyle \frac{x}{\sqrt{s}})^2}d(\frac{x}{\sqrt{s}}) \quad (\textrm{let}\,\, u=\frac{x}{\sqrt{s}})\\&=\frac{1}{\sqrt{s}}\arctan u\,\Big|_0^{\infin}\\&=\frac{\pi}{2}s^{-\frac{1}{2}}\end{aligned} F(s)=L[f(t)]​=∫0∞​L[e−x2t]t​dx=∫0∞​s+x21​dx=s ​1​∫0∞​1+(s ​x​)21​d(s ​x​)(letu=s ​x​)=s ​1​arctanu∣∣∣​0∞​=2π​s−21​​

对   F ( s )   作拉普拉斯反变换 \text{对}\,F(s)\,\text{作拉普拉斯反变换} 对F(s)作拉普拉斯反变换

   f ( t ) = L − 1 [ F ( s ) ] = π 2 L − 1 [ 1 s − 1 2 + 1 ] = π 2 1 Γ ( − 1 2 + 1 ) t − 1 2 = π 2 1 Γ ( 1 2 ) t − 1 2 \begin{aligned}f(t)=\mathscr{L}^{-1}[F(s)]&=\frac{\pi}{2}\mathscr{L}^{-1}[\frac{1}{s^{-\frac{1}{2}+1}}]\\&=\frac{\pi}{2}\frac{1}{\Gamma(-\frac{1}{2}+1)}t^{-\frac{1}{2}}\\&=\frac{\pi}{2}\frac{1}{\Gamma(\frac{1}{2})}t^{-\frac{1}{2}}\end{aligned} f(t)=L−1[F(s)]​=2π​L−1[s−21​+11​]=2π​Γ(−21​+1)1​t−21​=2π​Γ(21​)1​t−21​​

由余元公式： Γ ( s ) Γ ( 1 − s ) = π sin ⁡ π s . 令   s = 1 2 ，则    Γ ( 1 2 ) = π ， 则   f ( t ) = π 2 t   ,   ∫ 0 ∞ e − x 2 d x = f ( 1 ) = π 2   . \begin{aligned}&\text{由余元公式：}\Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin \pi s} .\\ &\text{令}\,s=\frac{1}{2}\text{，则}\,\,\Gamma(\frac{1}{2})=\sqrt{\pi}，\\&\text{则}\, f(t)=\frac{\sqrt{\pi}}{2\sqrt{t}}\,,\,\int_0^{\infin}e^{-x^2}dx=f(1)=\frac{\sqrt{\pi}}{2}\,.\end{aligned} ​由余元公式：Γ(s)Γ(1−s)=sinπsπ​.令s=21​，则Γ(21​)=π ​，则f(t)=2t ​π ​​,∫0∞​e−x2dx=f(1)=2π ​​.​

令   t = x 2 ，则   d t d x = 2 x = 2 t , d x = d t 2 t   . \begin{aligned}\text{令}\,t=x^2\text{，则}\,\frac{dt}{dx}=2x=2\sqrt{t} ,dx=\frac{dt}{2\sqrt{t}}\,.\end{aligned} 令t=x2，则dxdt​=2x=2t ​,dx=2t ​dt​.​ ∫ 0 ∞ e − x 2 d x = ∫ 0 ∞ e − t d t 2 t = 1 2 ∫ 0 ∞ e − t t 1 2 − 1 d t = 1 2   Γ ( 1 2 ) \int_{0}^{\infin}e^{-x^2}dx=\int_{0}^{\infin}e^{-t}\frac{dt}{2\sqrt{t}}=\frac{1}{2}\int_{0}^{\infin}e^{-t}t^{\frac{1}{2}-1}dt=\frac{1}{2}\,\Gamma(\frac{1}{2}) ∫0∞​e−x2dx=∫0∞​e−t2t ​dt​=21​∫0∞​e−tt21​−1dt=21​Γ(21​) 由上一种方法    Γ ( 1 2 ) = π ，则 ∫ 0 ∞ e − x 2 d x = π 2 . \begin{aligned}&\text{由上一种方法}\,\,\Gamma(\frac{1}{2})=\sqrt{\pi}\text{，则}\int_{0}^{\infin}e^{-x^2}dx=\frac{\sqrt{\pi}}{2}.\end{aligned} ​由上一种方法Γ(21​)=π ​，则∫0∞​e−x2dx=2π ​​.​

记   I = ∫ 0 ∞ e − x 2 d x ，令   x = u t ,   u > 0   为参数，则 \begin{aligned}\text{记}\,I=\int_0^{\infin}e^{-x^2}dx\text{，令}\,x=ut,\,u>0\,\text{为参数，则}\end{aligned} 记I=∫0∞​e−x2dx，令x=ut,u>0为参数，则​ I = u ∫ 0 ∞ e − u 2 t 2 d t e − u 2 I = e − u 2 u ∫ 0 ∞ e − u 2 t 2 d t \begin{aligned}I&=u\int_0^{\infin}e^{-u^2t^2}dt\\e^{-u^2}I&=e^{-u^2}u\int_0^{\infin}e^{-u^2t^2}dt\end{aligned} Ie−u2I​=u∫0∞​e−u2t2dt=e−u2u∫0∞​e−u2t2dt​ 两边对变量   u   积分， I ∫ 0 ∞ e − u 2 d u = ∫ 0 ∞ ( e − u 2 u ∫ 0 ∞ e − u 2 t 2 d t ) d u \begin{aligned}\text{两边对变量}\,u\,\text{积分，} I\int_0^{\infin}e^{-u^2}du&=\int_0^{\infin}\big(e^{-u^2}u\int_0^{\infin}e^{-u^2t^2}dt\big)du\\ \end{aligned} 两边对变量u积分，I∫0∞​e−u2du​=∫0∞​(e−u2u∫0∞​e−u2t2dt)du​ 右边交换积分次序， \begin{aligned}\text{右边交换积分次序，} \end{aligned} 右边交换积分次序，​

I 2 = 1 2 ∫ 0 ∞ ( ∫ 0 ∞ e − ( 1 + t 2 ) u 2 d u ) d t = 1 2 ∫ 0 ∞ 1 1 + t 2 d t = 1 2 arctan ⁡ t   ∣ 0 ∞ = π 4 \begin{aligned}I^2&=\frac{1}{2}\int_0^{\infin}\big(\int_0^{\infin}e^{-(1+t^2)u^2}du\big)dt\\&=\frac{1}{2}\int_0^{\infin}\frac{1}{1+t^2}dt \\&=\frac{1}{2}\arctan t\,\Big|_0^{\infin}\\&=\frac{\pi}{4}\end{aligned} I2​=21​∫0∞​(∫0∞​e−(1+t2)u2du)dt=21​∫0∞​1+t21​dt=21​arctant∣∣∣​0∞​=4π​​

所以   I = π 2   . \begin{aligned}\text{所以}\,I=\frac{\sqrt{\pi}}{2}\,.\end{aligned} 所以I=2π ​​.​

记   I = ∫ 0 ∞ e − x 2 d x   .   令   f ( x ) = ∫ 0 1 e − x ( 1 + t 2 ) 1 + t 2 d t ,   x ≥ 0 ，则 \begin{aligned}\text{记}\,I=\int_0^{\infin}e^{-x^2}dx\,. \,\text{令}\,f(x)=\int_0^{1}\frac{e^{-x(1+t^2)}}{1+t^2}dt,\,x\geq 0\text{，则}\end{aligned} 记I=∫0∞​e−x2dx.令f(x)=∫01​1+t2e−x(1+t2)​dt,x≥0，则​     f ( 0 ) = ∫ 0 1 1 1 + t 2 d t = arctan ⁡ t   ∣ 0 1 = π 4 f ( ∞ ) = lim ⁡ x → ∞ ∫ 0 1 e − x ( 1 + t 2 ) 1 + t 2 d t = 0 \begin{aligned} &f(0)=\int_0^{1}\frac{1}{1+t^2}dt=\arctan t\,\Big|_0^1=\frac{\pi}{4} \\ &f(\infin)=\lim_{x\to\infin}\int_0^{1}\frac{e^{-x(1+t^2)}}{1+t^2}dt=0\end{aligned} ​f(0)=∫01​1+t21​dt=arctant∣∣∣​01​=4π​f(∞)=x→∞lim​∫01​1+t2e−x(1+t2)​dt=0​

    f ′ ( x ) = − ∫ 0 1 ∂ ∂ x ( e − x ( 1 + t 2 ) 1 + t 2 ) d t = − ∫ 0 1 e − x ( 1 + t 2 ) d t = − e − x ∫ 0 1 e − x t 2 d t ( l e t    u = x t ,   d t = d u / x   ) = − e − x x ∫ 0 x e − u 2 d u \begin{aligned}f'(x)&=-\int_0^1\frac{\partial }{\partial x}\Big(\frac{e^{-x(1+t^2)}}{1+t^2}\Big)dt\\&=-\int_0^{1}e^{-x(1+t^2)}dt \\ &=-e^{-x}\int_0^{1}e^{-xt^2}dt \quad (let\,\,u=\sqrt{x}t,\,dt=du/\sqrt{x}\,) \\&=-\frac{e^{-x}}{\sqrt{x}}\int_0^{\sqrt{x}}e^{-u^2}du\end{aligned} f′(x)​=−∫01​∂x∂​(1+t2e−x(1+t2)​)dt=−∫01​e−x(1+t2)dt=−e−x∫01​e−xt2dt(letu=x ​t,dt=du/x ​)=−x ​e−x​∫0x ​​e−u2du​

记    g ( x ) = ∫ 0 x e − t 2 d t   , 则   f ′ ( x ) = − e − x x g ( x ) ,   g ′ ( x ) = e − x 2 ,   g ( 0 ) = 0 ,   g ( ∞ ) = I . \begin{aligned}&\text{记}\,\,g(x)=\int_0^{x}e^{-t^2}dt\,,\\&\text{则} \, f'(x)=-\frac{e^{-x}}{\sqrt{x}}g(\sqrt{x}),\,g'(x)=e^{-x^2},\,g(0)=0,\,g(\infin)=I.\end{aligned} ​记g(x)=∫0x​e−t2dt,则f′(x)=−x ​e−x​g(x ​),g′(x)=e−x2,g(0)=0,g(∞)=I.​

由牛顿-莱布尼兹公式， \begin{aligned}\text{由牛顿-莱布尼兹公式，}\end{aligned} 由牛顿-莱布尼兹公式，​

    f ( ∞ ) − f ( 0 ) = ∫ 0 ∞ f ′ ( x ) d x = − ∫ 0 ∞ e − x x g ( x ) d x ( let   u = x ,   d u = d x 2 x ) = − 2 ∫ 0 ∞ e − u 2 g ( u ) d u = − 2 ∫ 0 ∞ g ( u ) g ′ ( u ) d u = − 2 ∫ 0 ∞ g ( u ) d ( g ( u ) ) = − ∫ 0 ∞ d ( g ( u ) 2 ) = g ( 0 ) 2 − g ( ∞ ) 2 \begin{aligned}f(\infin)-f(0)&=\int_0^{\infin}f'(x)dx\\&=-\int_0^{\infin}\frac{e^{-x}}{\sqrt{x}}g(\sqrt{x})dx\quad (\textrm{let} \,u=\sqrt{x},\,du=\frac{dx}{2\sqrt{x}} )\\&=-2\int_0^{\infin}e^{-u^2}g(u)du\\&=-2\int_0^{\infin}g(u)g'(u)du\\&=-2\int_0^{\infin}g(u)d(g(u))\\&=-\int_0^{\infin}d\big(g(u)^2\big)\\&=g(0)^2-g(\infin)^2 \end{aligned} f(∞)−f(0)​=∫0∞​f′(x)dx=−∫0∞​x ​e−x​g(x ​)dx(letu=x ​,du=2x ​dx​)=−2∫0∞​e−u2g(u)du=−2∫0∞​g(u)g′(u)du=−2∫0∞​g(u)d(g(u))=−∫0∞​d(g(u)2)=g(0)2−g(∞)2​

所以， 0 − π 4 = 0 − I 2 ,   I = π 2   . \begin{aligned}\text{所以，} 0-\frac{\pi}{4}&=0-I^2,\,I=\frac{\sqrt{\pi}}{2}\,.\end{aligned} 所以，0−4π​​=0−I2,I=2π ​​.​

Wallis 公式内容： \begin{aligned}\text{Wallis 公式内容：}\end{aligned} Wallis 公式内容：​ lim ⁡ n → ∞ ( 2 n − 1 ) ! ! ( 2 n ) ! ! 2 n = 2 π \lim_{n\to\infin}\frac{(2n-1)!!}{(2n)!!}\sqrt{2n}=\sqrt{\frac{2}{\pi}} n→∞lim​(2n)!!(2n−1)!!​2n ​=π2​ ​ 推导过程参见： \text{推导过程参见：} 推导过程参见：Wallis公式_百度百科

   ∵   lim ⁡ n → ∞ ( 1 + x 2 n ) n x 2 = e ∴   lim ⁡ n → ∞ ( 1 + x 2 n ) − n = e − x 2 \begin{aligned}\because \,\lim_{n\to\infin} \Big(1+\frac{x^2}{n}\Big)^{\frac{n}{x^2}}&=e\\ \therefore \,\lim_{n\to\infin} \Big(1+\frac{x^2}{n}\Big)^{-n}&=e^{-x^2}\end{aligned} ∵n→∞lim​(1+nx2​)x2n​∴n→∞lim​(1+nx2​)−n​=e=e−x2​

  ∫ 0 ∞ e − x 2 d x = ∫ 0 ∞ lim ⁡ n → ∞ ( 1 + x 2 n ) − n d x = lim ⁡ n → ∞ ∫ 0 ∞ ( 1 + x 2 n ) − n d x \begin{aligned}\int_0^{\infin}e^{-x^2}dx=&\int_0^{\infin}\lim_{n\to\infin} \Big(1+\frac{x^2}{n}\Big)^{-n}dx =\lim_{n\to\infin} \int_0^{\infin}\Big(1+\frac{x^2}{n}\Big)^{-n}dx \end{aligned} ∫0∞​e−x2dx=​∫0∞​n→∞lim​(1+nx2​)−ndx=n→∞lim​∫0∞​(1+nx2​)−ndx​

  ( 可以验证积分与极限次序是可交换的 ) . \begin{aligned}\\&(\text{可以验证积分与极限次序是可交换的}).\end{aligned} ​(可以验证积分与极限次序是可交换的).​

令   tan ⁡ t = x n ，则   d t d x = 1 n ( 1 + x 2 n ) − 1 ,   d x = n ( 1 + x 2 n ) d t . \begin{aligned}\text{令}\,\tan t=\frac{x}{\sqrt{n}} \text{，则}\,\frac{dt}{dx}=\frac{1}{\sqrt{n}}(1+\frac{x^2}{n})^{-1},\, dx=\sqrt{n}(1+\frac{x^2}{n})dt.\end{aligned} 令tant=n ​x​，则dxdt​=n ​1​(1+nx2​)−1,dx=n ​(1+nx2​)dt.​ 原式 = lim ⁡ n → ∞ ∫ 0 π 2 n ( 1 + x 2 n ) − n + 1 d t = lim ⁡ n → ∞ ∫ 0 π 2 n ( 1 + ( tan ⁡ t ) 2 ) − ( n − 1 ) d t = lim ⁡ n → ∞ n ∫ 0 π 2 ( cos ⁡ t ) 2 n − 2 d t ( ∫ 0 π 2 ( cos ⁡ t ) 2 n d t = ( 2 n − 1 ) ! ! ( 2 n ) ! ! π 2   ) = lim ⁡ n → ∞ n   ( 2 n − 3 ) ! ! ( 2 n − 2 ) ! ! π 2 = π 2 lim ⁡ n → ∞ ( n − 1 ) + 1   ( 2 ( n − 1 ) − 1 ) ! ! ( 2 ( n − 1 ) ) ! ! ( let    n ′ = n − 1 ) = π 2 lim ⁡ n ′ → ∞ n ′ + 1 2 n ′   ( 2 n ′ − 1 ) ! ! ( 2 n ′ ) ! ! 2 n ′ = π 2 2 lim ⁡ n ′ → ∞ n ′ + 1 n ′ lim ⁡ n ′ → ∞ ( 2 n ′ − 1 ) ! ! ( 2 n ′ ) ! ! 2 n ′ = π 2 2 ⋅ 1 ⋅ 2 π = π 2 \begin{aligned} \text{原式}&=\lim_{n\to\infin} \int_0^{\frac{\pi}{2}}\sqrt{n}(1+\frac{x^2}{n})^{-n+1}dt \\&=\lim_{n\to\infin} \int_0^{\frac{\pi}{2}}\sqrt{n}(1+(\tan t)^2)^{-(n-1)}dt\\&=\lim_{n\to\infin} \sqrt{n}\int_0^{\frac{\pi}{2}}(\cos t)^{2n-2}dt \quad \Big( \int_0^{\frac{\pi}{2}}(\cos t)^{2n}dt=\frac{(2n-1)!!}{(2n)!!}\frac{\pi}{2}\,\Big)\\&=\lim_{n\to\infin} \sqrt{n}\,\frac{(2n-3)!!}{(2n-2)!!}\frac{\pi}{2} \\&=\frac{\pi}{2}\lim_{n\to\infin} \sqrt{(n-1)+1}\,\frac{(2(n-1)-1)!!}{(2(n-1))!!} \quad (\textrm{let}\,\,n'=n-1)\\&=\frac{\pi}{2}\lim_{n'\to\infin} \frac{\sqrt{n'+1}}{\sqrt{2n'}}\,\frac{(2n'-1)!!}{(2n')!!}\sqrt{2n'}\\&=\frac{\pi}{2\sqrt{2}}\lim_{n'\to\infin} \frac{\sqrt{n'+1}}{\sqrt{n'}}\lim_{n'\to\infin} \frac{(2n'-1)!!}{(2n')!!}\sqrt{2n'}\\&=\frac{\pi}{2\sqrt{2}}\cdot1\cdot\sqrt{\frac{2}{\pi}}\\&=\frac{\sqrt{\pi}}{2}\end{aligned} 原式​=n→∞lim​∫02π​​n ​(1+nx2​)−n+1dt=n→∞lim​∫02π​​n ​(1+(tant)2)−(n−1)dt=n→∞lim​n ​∫02π​​(cost)2n−2dt(∫02π​​(cost)2ndt=(2n)!!(2n−1)!!​2π​)=n→∞lim​n ​(2n−2)!!(2n−3)!!​2π​=2π​n→∞lim​(n−1)+1 ​(2(n−1))!!(2(n−1)−1)!!​(letn′=n−1)=2π​n′→∞lim​2n′ ​n′+1 ​​(2n′)!!(2n′−1)!!​2n′ ​=22 ​π​n′→∞lim​n′ ​n′+1 ​​n′→∞lim​(2n′)!!(2n′−1)!!​2n′ ​=22 ​π​⋅1⋅π2​ ​=2π ​​​

所以   ∫ 0 ∞ e − x 2 d x = π 2 . \begin{aligned}\text{所以}\,\int_0^{\infin}e^{-x^2}dx=\frac{\sqrt{\pi}}{2}\end{aligned}. 所以∫0∞​e−x2dx=2π ​​​.

若读者还有其他巧妙解法，请不吝赐教！ \small \text{若读者还有其他巧妙解法，请不吝赐教！} 若读者还有其他巧妙解法，请不吝赐教！

文末彩蛋：大家好，这是我的孪生兄弟： \small \textbf{文末彩蛋：大家好，这是我的孪生兄弟：} 文末彩蛋：大家好，这是我的孪生兄弟： 无穷积分   ∫ sin ⁡ x x d x   的几种巧妙解法！ \small \textbf{无穷积分}\,\displaystyle \int \frac{\sin x}{x}dx\, \textbf{的几种巧妙解法！} 无穷积分∫xsinx​dx的几种巧妙解法！

Plus: 如有错误、可以改进的地方、或任何想说的，请在评论区留言！